バイスタティックRCSモデリングによる異方性球体散乱解析
この例は、XFdtdが誘電率テンソルの非対角項を持つ誘電体をシミュレートできることを示しています。ここでは、平面波によって励起された異方性球からのバイスタティックレーダー断面積の計算を例にしています。
球の大きさはka = 0.5とし、kは2π/λで与えられる波数で、λは自由空間の波長である。このシミュレーションでは、周波数を300MHzとし、波長を1mとします。この例で検討している材料の誘電率は、周波数領域で次式で与えられるテンソルを持ちます:

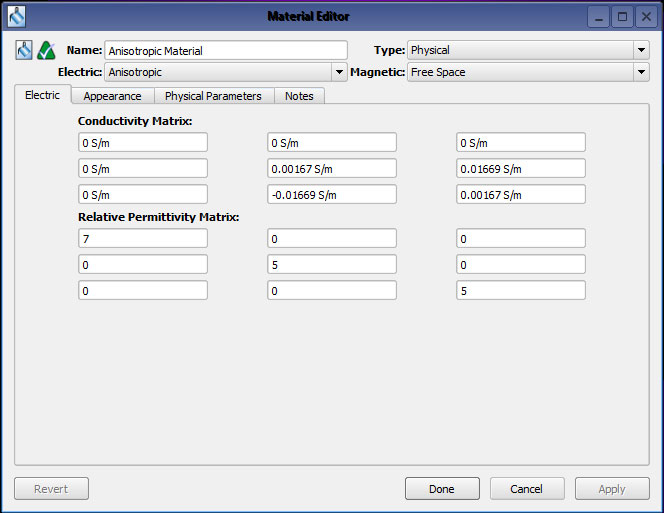
図1:異方性材料を定義したXFdtdマテリアルエディター。
300 MHzでは、項(5 - 0.1j)は誘電率5、導電率0.00167 S/mに変換される。同様に、非対角項 (+/- j) の導電率は+/- 0.01669 S/m に変換されます。この材料を XF7 材料エディタに入力した図を図 1 に示します。この材料は対角上の虚数項によりわずかに損失があります。非対角の虚数項は符号が逆であるため、材料に損失を加えることはありませんが、ジャイロトロピックになります。
XFdtdで適当な大きさの球を作成し、5mmグリッドでメッシュ化する。周波数300MHzの平面波が-X方向(θ=90度、φ=180度)から入射し、電場はZ偏極(θ方向)します。この励起では、もし材料が斜め等方性であれば、Y偏光電場は存在しない。
比較のため、誘電率5の等方性球について初期計算を行った。E面およびH面の双安定散乱パターンを等方性球について計算し、図2および図3に示す。E面パターンでは、球のXZ面を中心にθの角度変化があり、波は270度から入射している。H面パターンでは、XY面を中心にφで変化しており、波は180度の方向から入射している。同偏波のプロットは図に見えるが、交差偏波の信号は非常に小さいので、プロットには現れない。これは等方性球面での予想通りです。
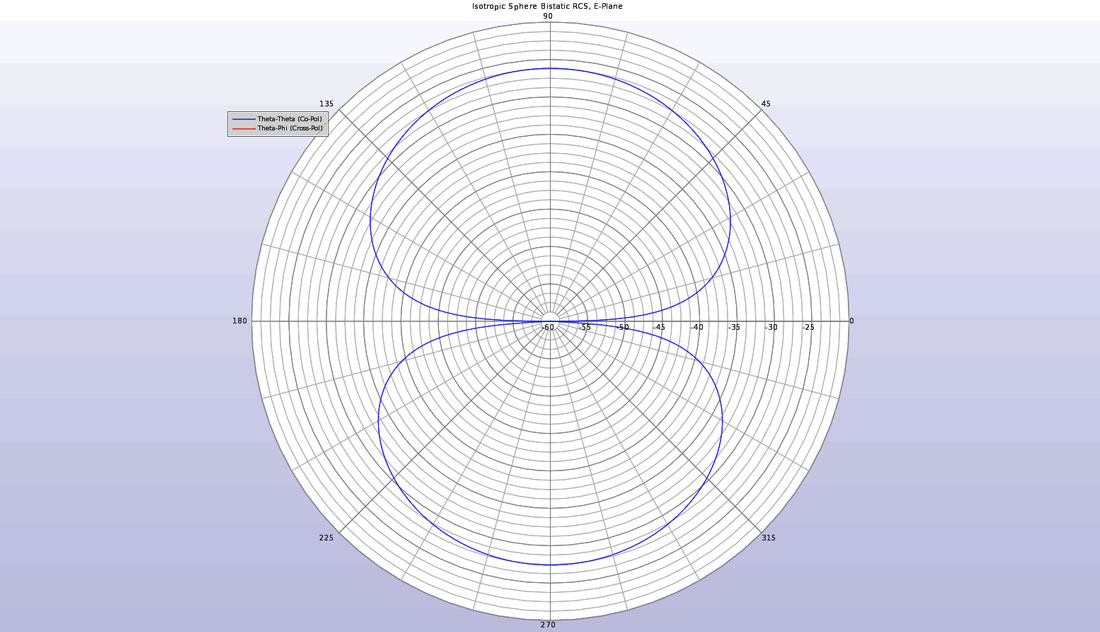
図2:E面における等方性球体のバイスタティックRCSは、同偏光散乱のみを示す。
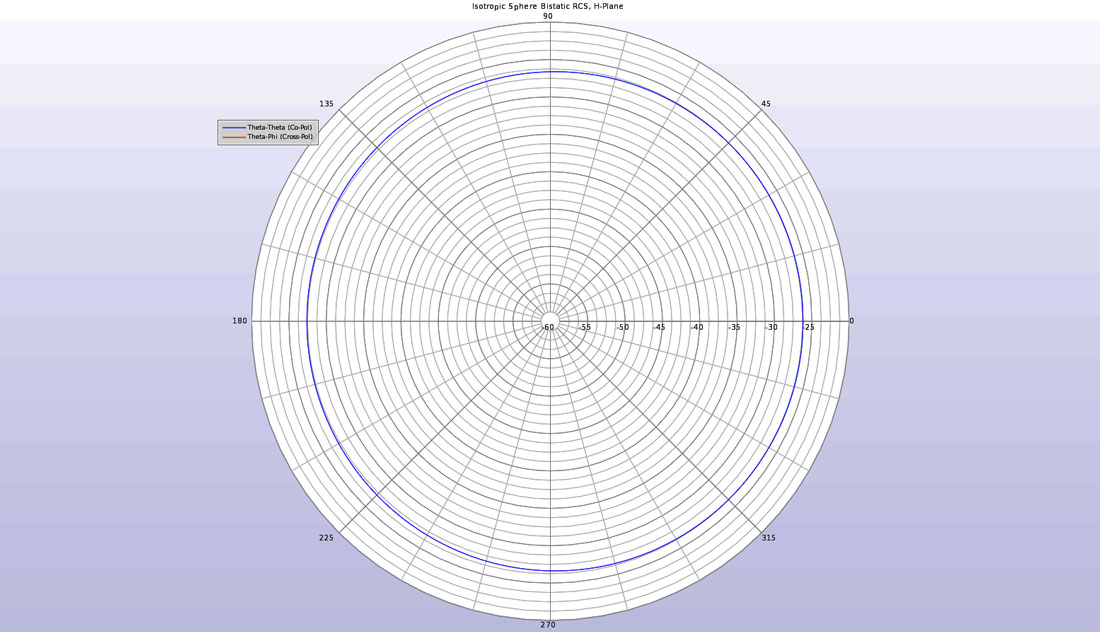
図3:H面における等方性球のバイスタティックRCSは、同偏波散乱のみを示す。
異方性球を等方性球に置き換えると、得られる出力は異なる。図4と図5からわかるように、バイスタティック散乱パターンには、同偏光信号に加え、交差偏光成分が見られます。交差偏光パターンは、材料の異方性の結果である。
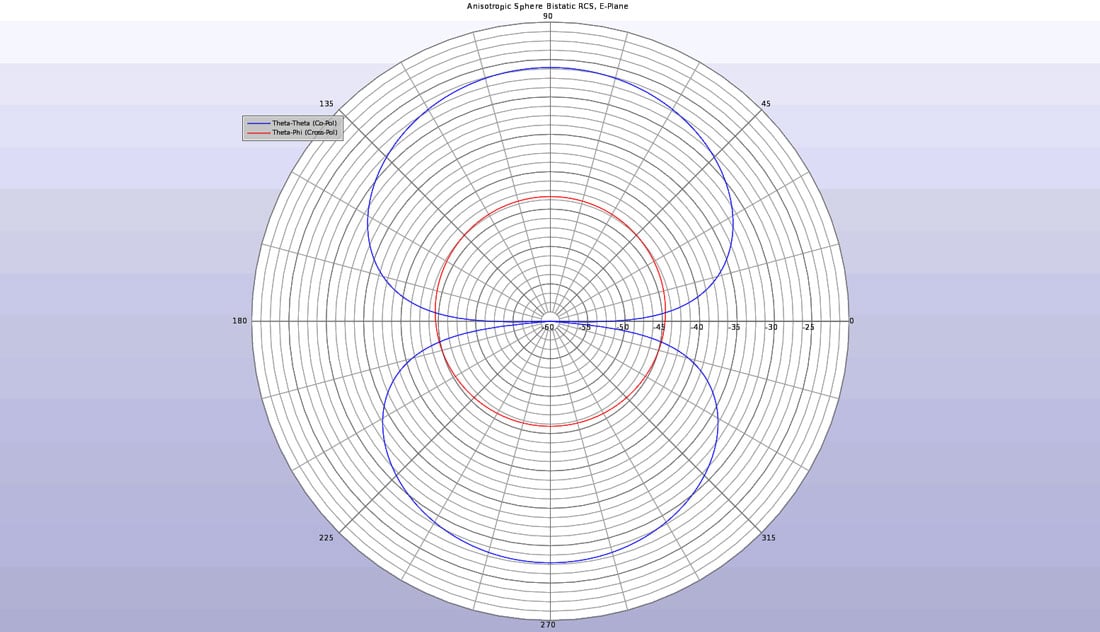
図4: E面における異方性球体のバイスタティックRCS。
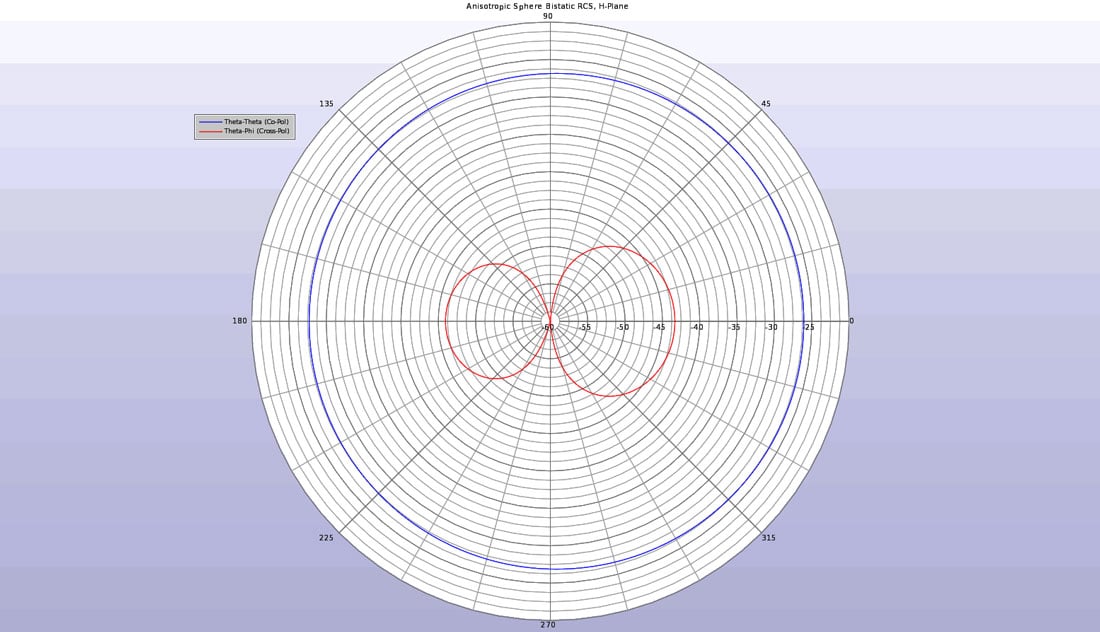
図5: H平面における異方性球体のバイスタティックRCS。
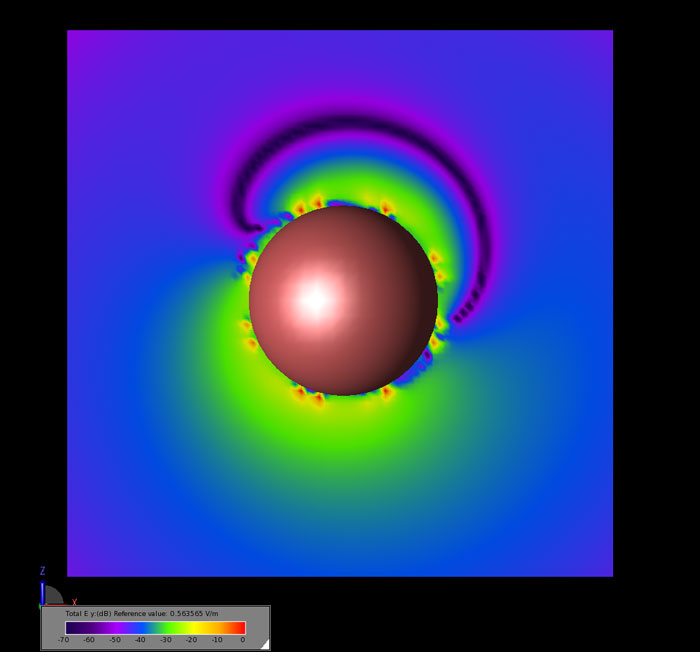
ニアフィールドでは、異方性球のY偏光電場が見える。図6では、定常状態の電界の大きさが、異方性球の周りのE平面上の電界のY成分について表示されている。