- 方法
- 有限差分時間領域法 (FDTD)
FDTD法 電磁界シミュレーションのための
FDTD アプローチは,問題のサイズが大きくなるにつれて,手法の優れたスケーリング性能を提供します.未知数の数が増加するにつれて、FDTD アプローチは、効率性において他の手法をすばやく上回ります。
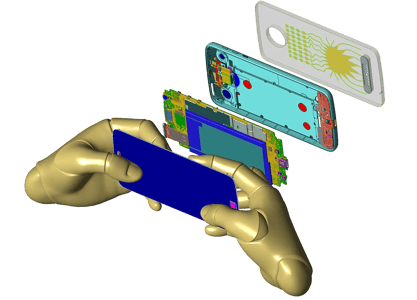
携帯電話の機種はMotorola Mobility, LLC/Lenovoの提供によるものです。
度線流体力学シミュレーション・ソフトウェアを度線流体力学シミュレーション・ソフトウェアを度線流体力学シミュレーション・度線流体力学シミュレーション
多くの電磁界シミュレーション技術が周波数領域で適用されるのに対し、FDTDは時間領域でマクスウェル方程式を解きます。これは、電磁界値の計算が時間的に離散的なステップで進行することを意味します。時間領域アプローチの利点の1つは、プログラムの1回の実行で広帯域の出力が得られることです。しかし、FDTDアプローチを使用する主な理由は、問題のサイズが大きくなるにつれて、この手法が優れたスケーリング性能を発揮することです。未知数の数が増加するにつれて、FDTD アプローチは、効率性において他の手法をすばやく上回ります。また,FDTD 法は,無線機器からの生物学的影響に対す る電磁気シミュレーションの実行に適した手法であるこ とも確認されています[1].FDTD 法は、最も効率的なアプローチであり、生体組織への電界の侵入について正確な結果が得られることが示されています。
度線流体力学シミュレーションのの度線流体力学シミュレーションの度線流体力学シミュレーション
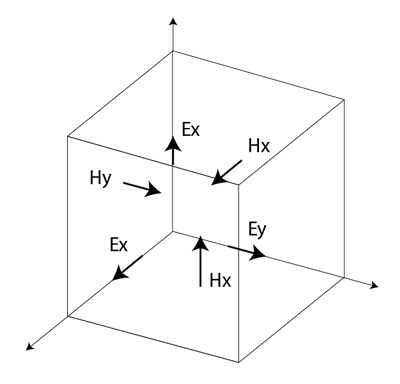
FDTD法ではではではではではではでは露骨なのの露光時間ではFDTD法では露光時間分割法では露光時間分割法では露光時間分割法では露光時間分割法では露光時間分割法。空間は、波長に比べて小さな箱型のセルに分割されます。図 1 に示すように、電場は箱の縁に、磁場は面に配置されます。このような磁場の向きはYeeセル[2, p.37]として知られ、FDTDの基礎となっています。時間は小さなステップに量子化され、各ステップは磁場があるセルから次のセルに移動するのに必要な時間を表します。磁場が電場から空間的にオフセットしているため、時間に対する磁場の値もオフセットしています。電場と磁場は、まず電場が計算され、次に磁場が各ステップで計算されるリープフロッグ方式で更新されます。
多数のFDTDセルを組み合わせて3次元の体積を形成すると、FDTDグリッドまたはメッシュになります。各 FDTD セルは隣接するセルとエッジや面が重なるため、 慣例的に各セルはそのセルに関連する共通のノードから始まる 3 つの電場を持つことになります。FDTDセルの他の9つのエッジの電場は、他の隣接するセルに属します。各セルは、図1に示すように、電界の共通ノードに隣接するセルの面を起点とする3つの磁界も持つことになります。
メッシュ内に、導体や誘電体のような物質を追加するには、与えられた位置の電界を計算する方程式を変更します。例えば、セルエッジに完全導電性のワイヤーセグメントを追加する場合、完全導電体の電界は同じようにゼロであるため、電界を計算する方程式を単純にゼロに設定することで置き換えることができます。完全導電材料として定義された多数の端から端までのセル・エッジを接合することで、ワイヤーを形成することができる。他の材料や他の構成を導入する場合も同様に処理され、材料の特性に応じて電界または磁界のいずれかにそれぞれ適用することができる。多くのセルエッジを材料と関連付けることで、図2に示す誘電体球のような幾何学的構造をFDTDグリッド内に形成することができます。図中の小さなボックスは、それぞれ1つのFDTDセルを表しています。
のののののののののののののののののののののののののののののののののののののの屈指の

図2:階段状の従来のFDTDグリッドでメッシュ化された誘電体球。個々のセルエッジ(電界位置)は、重なり合ったグリッド線として表示されている。
セルサイズ(小さな箱の寸法)は、時間のステップサイズだけでなく、計算の上限周波数も決定するため、FDTDシミュレーションにおいて最も重要な制約です。一般的な経験則では、最小分解能、ひいては上限周波数を1波長あたり10セルに設定しています。実際には、基板の厚さやワイヤの長さなど、シミュレートする構造の寸法や特徴を分解するために、セルサイズはこれよりも小さくなることがよくあります。
励起は、さまざまな方法で FDTD シミュレーションに適用できます。その 1 つの方法は、1 つまたは複数の位置でフィールド更新方程式にサンプリング波形を適用することによって、離散的な位置でジオメトリを励起するエミュレートです。時間の各ステップで、その時間の波形の値が場の値に追加されます。周囲の場は、各セルの特性に応じて、導入された波形をFDTDグリッド全体に適切に伝播させます。計算は収束状態に達するまで続けなければなりません。これは通常、すべての電界値が実質的にゼロ(ピークから少なくとも60dBダウン)に減衰したか、定常状態に達したことを意味します。
セル階段の進歩
伝統的に、階段状のFDTDセルは煩雑で、曲面や大きく変化する場の解像度が低いと考えられてきました。FDTDの進歩により、コンフォーマルメッシュと特異点補正が可能になりました。
図1のキュービクル・イーセルは一般に長方形である。x, y, z 方向のセル間の間隔は、問題空間全体で変えることができます。これにより、導電性の高い材料の小さなフィーチャーの周りなど、強磁場の領域でより多くのセルエッジを配置することができます。セル内では、FDTDの標準的な更新方程式をさまざまな方法で改良することができます。たとえば、セルサイズよりも細いワイヤを許容したり、マイクロストリップ線路のような導体のエッジの強電界を計算したりすることができます。また、別の改良を加えることで、主軸に対して任意の角度でセルと交差する表面を持つ物体を許容することができます。これらの "コンフォーマル "セルは、セル体積内の物体表面の曲率を考慮するためにさらに改良することができる。
図3は携帯電話の一部の形状を示している。分かりやすくするために、外側のケースを含む多くの部品の視認性をオフにし、アンテナ近傍の領域を示しています。図4aには、単純な矩形セルを使用した携帯電話のFDTDメッシュの一部が示されています。図4bでは、電話機のメッシュの同じ部分を示していますが、今回は物体の表面の一部を含むセルに対して、一種のコンフォーマル処理を使用しています。図5は、コンフォーマルメッシュの表面の拡大図である。
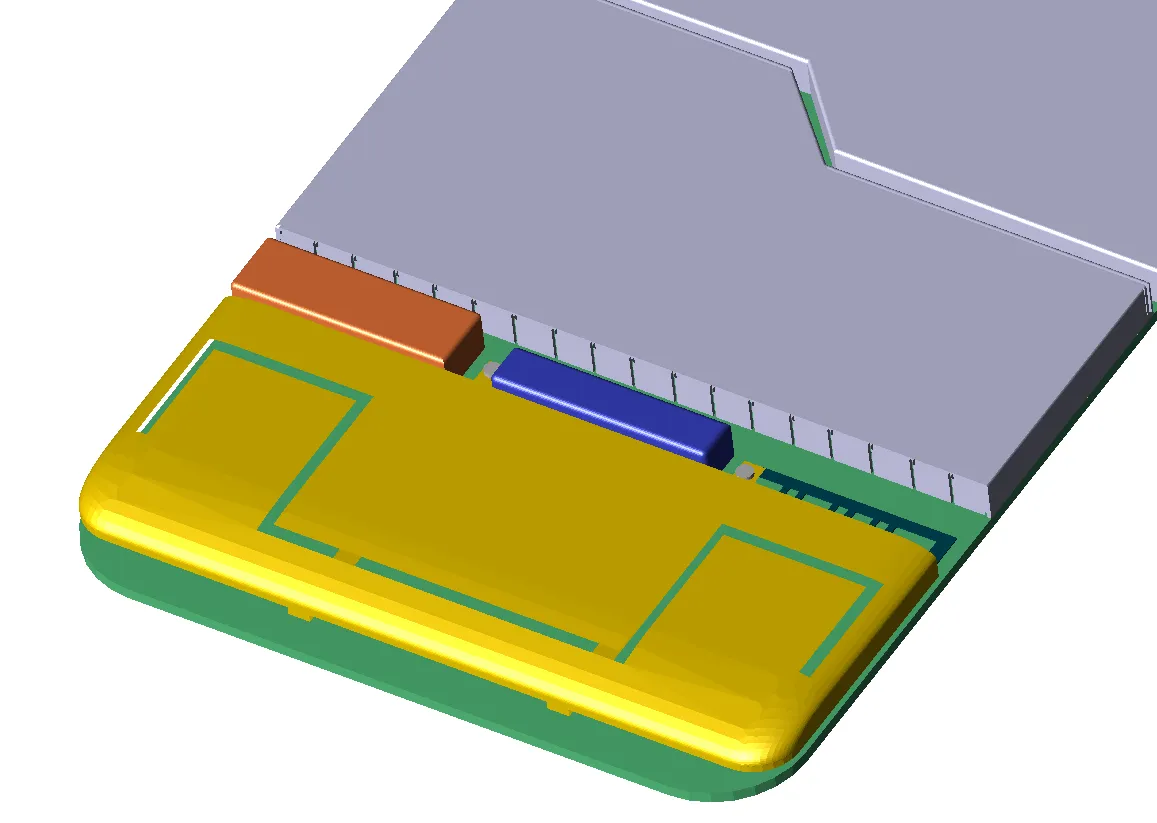
図3:携帯電話のアンテナ部。
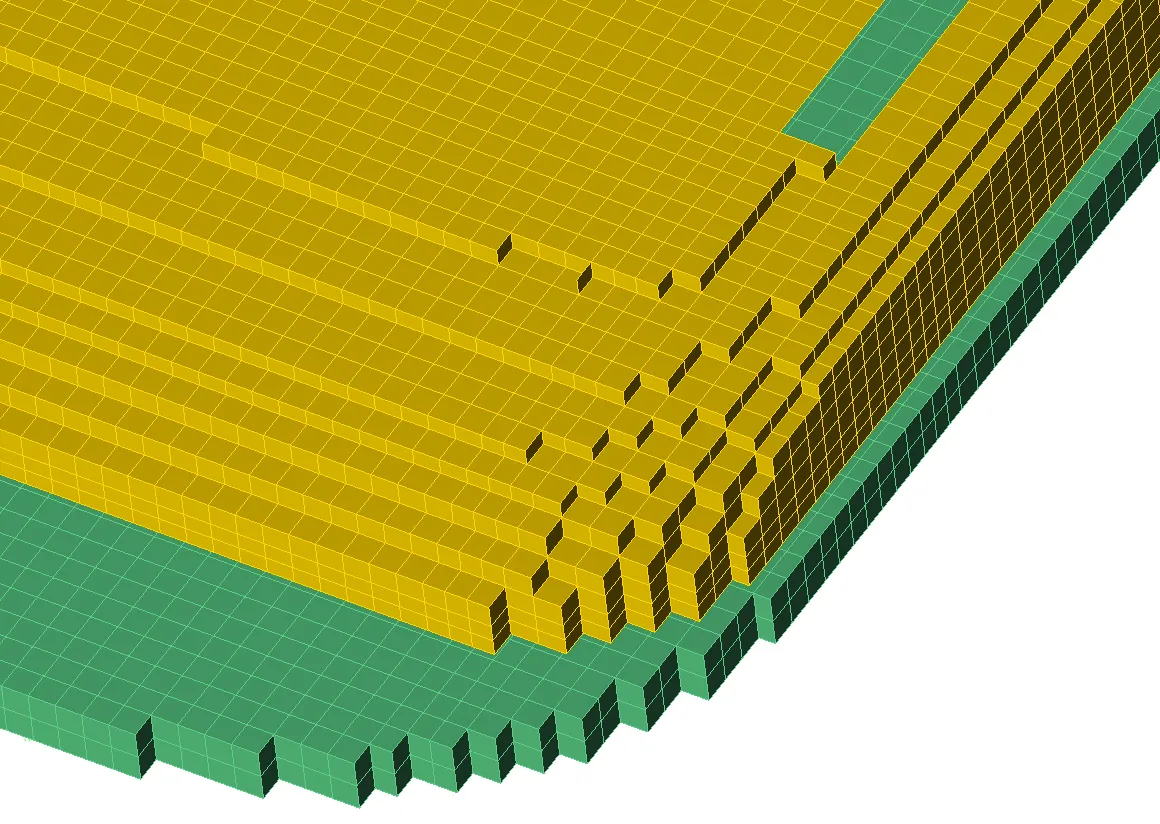
図4a:単純な長方形メッシュを使用したアンテナのコーナーのメッシュ図。

図4b:コンフォーマルメッシュを使ったアンテナのコーナーのメッシュ図。
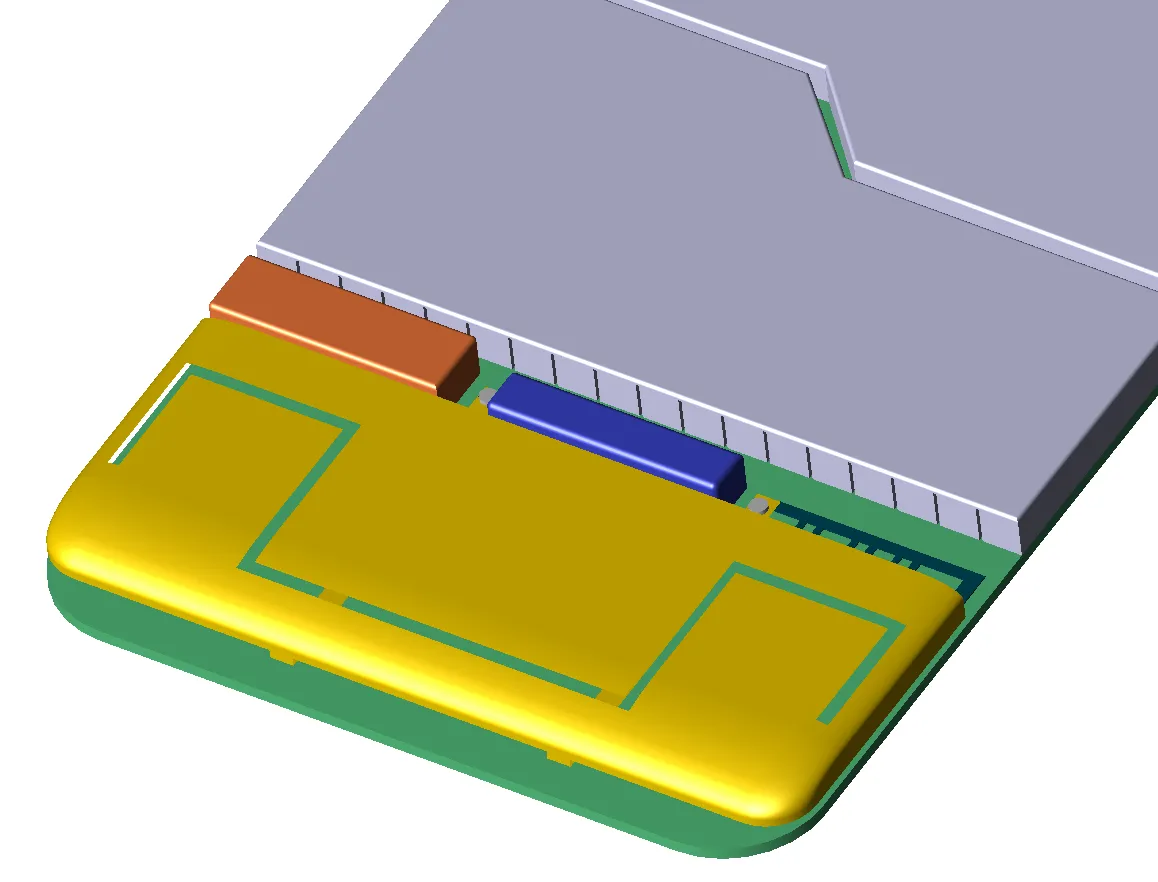
図5:携帯電話アンテナのコンフォーマルメッシュ。
材料
FDTDシミュレーション・ソフトウェアは、様々な電気・磁気材料のシミュレーションが可能です。もちろん、最も基本的な材料は自由空間です。すべてのFDTDセルは自由空間として初期化され、自由空間に代わる別の材料が追加されない限り、すべてのセルエッジのフィールドは自由空間の方程式を使用して更新されます。
完全導電材料や完全磁性材料は、これらの材料内にあるセルエッジの電界や磁界をゼロに設定することでシミュレートされます。これらの材料は計算が簡単なため、可能な限り、実際の導体よりも完全導体を使用した方がよいでしょう。銅のような導体もFDTDでシミュレートできますが、銅材料の場の計算式は完全導体の場合よりも複雑になるため、計算に時間がかかります。もちろん、FDTDセルのごく一部しか導体として定義されていないようなケースでは、実行時間の差はほとんど気にならないでしょう。
周波数に依存しない誘電体および磁性材料は、電気材料では比誘電率と導電率または損失正接、磁性材料では比透磁率と磁気伝導率の構成パラメータによって定義されます。多くの場合、広帯域計算を行う場合でも、パラメータが周波数範囲にわたって大きく変化しないため、これらの材料が適切です。
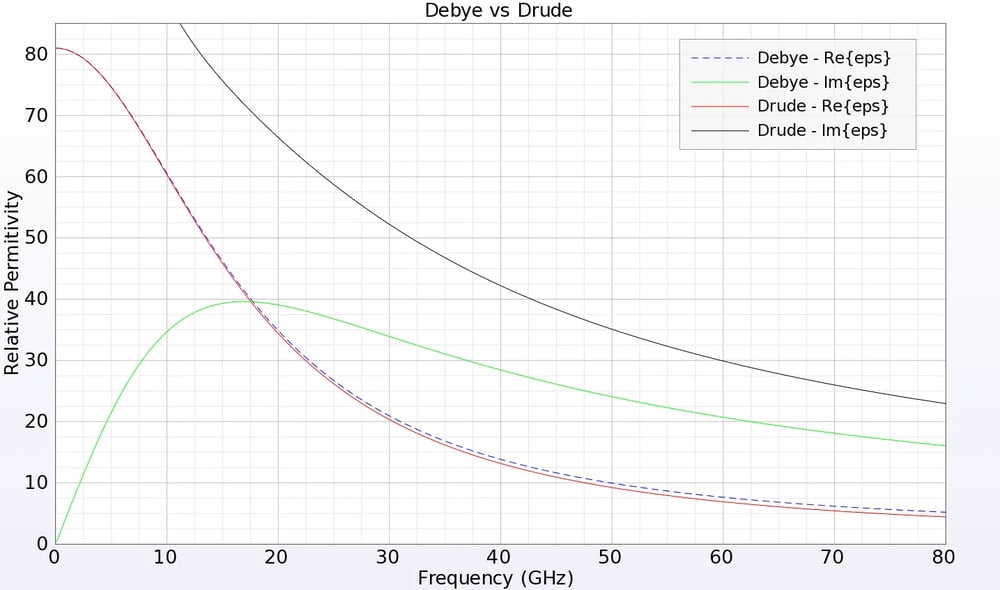
場合によっては、周波数に依存しない材料は適切でなく、代わりに周波数に依存する材料、つまり分散性のある材料を代用すべきである。周波数依存性材料の一般的な例としては、人体組織のような含水率の高い材料、光周波数で励起される金属、広帯域にわたる誘電体などがあります。XFdtdには、周波数に依存しない異方性誘電体だけでなく、プラズマ、ローレンツ材料、異方性磁性フェライトなどの電気的および磁気的なデバイおよびドリュード材料のシミュレーション機能も含まれています。これらの材料は、周波数によっては負の誘電率や透磁率を持つことがあり、メタマテリアルを巨視的にシミュレートするのに有効です。また、FDTDは非線形材料のシミュレーションにも特に有効で、XFdtdにはいくつかの非線形材料が含まれています。
ニアゾーンとファーゾーン
どのような計算でも、特定の位置のセルエッジを特定の材料に設定することで、シミュレートされる構造の形状が定義されます。一般にグリッドまたはメッシュと呼ばれるFDTDジオメトリ空間全体は、これらのセルの3次元ブロックで構成されます。この3次元の体積は、FDTDではデータ保存の観点からニアゾーン領域とみなされます。FDTDグリッドの任意のエッジにおけるフィールド値は、XFdtdに「ニアゾーン」ポイントを保存することで、時間の関数として観察することができます。定常状態の電界の大きさ、比吸収率、S パラメータ、またはインピーダンスなどの他のタイプのデータも、グリッド内の適切な点、面、および体積に対して保存することができます。
ジオメトリの遠視野の点をサンプリングするのに十分な大きさの FDTD グリッドを作成することは可能です。一般的に、未知数(セル)の数が多くなる可能性が高いため、コンピュータのメモリと計算時間の点で非常にコストがかかります。FDTDの各セルの最大サイズは波長の10分の1であるため、構造から何波長も離れると、多数のセルが必要になることに注意してください。ほとんどの場合、これは遠視野結果をモニターする方法としては適切ではありません。
フィールド値をファーゾーンに変換し、放射利得やレーダー散乱パターンを計算するためのより実用的な方法は、FDTDグリッド内のニアゾーン値をグリッドから離れた位置のファーフィールド値に変換する変換を使用することです。これは、ジオメトリをボックスで囲み、このボックスの外側の面にフィールドを格納することで、一般的なファーゾーン問題に対応します。ボックスの面は、FDTDグリッドの各外縁から5つのFDTDセルに位置しています。変換が有効であるためには、FDTDジオメトリのすべての部分がボックス内に含まれている必要があります。
XFdtdで使用される極座標系は、図6に示すように、方位角(phi)をx軸から、仰角(θ)をz軸から参照して定義される。この座標系は、ファーゾーンの位置の特定と、平面波の入射方向の定義に使用されます。
.webp?width=269&height=254&name=image-asset%20(4).webp)
図6:ファーゾーンと入射平面波の方向に使用される極座標系。
広帯域と定常状態の計算
一般に、FDTDでは広帯域計算が実行されます。なぜなら、1回の計算で、余分なコンピュータリソースを必要とせずに、広範囲の周波数に対する結果を得ることができるからです。特定の周波数のデータが必要な場合は、フーリエ変換によって広帯域計算から定常状態のデータを計算することができます。
データ対周波数の一般的な例としては、特定の周波数におけるアンテナパターン、比吸収率(SAR)などの生物学的アプリケーション、電界と磁界の大きさ、磁束の大きさ、伝導電流、Sパラメータ、群遅延、インピーダンス、パワー、効率などの「回路」タイプの情報などがある。
正弦波励振が望まれるのは、特定の場合であり、例えば、目的の周波数範囲の外側にあるが、その近くにある強い共振を避ける場合などである。
放射線の外側境界
セルの3次元グリッドがFDTDジオメトリを形成し、各セル位置で更新される場は隣接する場に依存する。しかし、メモリの制限により、グリッドはある点で終了しなければならず、このため、グリッドの外縁の場は正しく更新されません。この状況を修正するために、FDTDグリッドの端に外側輻射境界条件が適用されます。
外側放射境界は、FDTDグリッドから境界に向かって伝搬する場を吸収する方法である。これらの場を吸収することで、グリッドは永遠に広がっているように見えます。外部境界の性能は、FDTD計算の精度を左右する重要な要素であり、正しく使用するように注意する必要があります。
場合によっては、吸収境界よりも反射境界の方が好ましいこともあります。FDTD 計算では、問題の対称性を利用するために、完全導電境界(電 界または磁気界)を使用して場をイメージ化することができます。周期境界条件は、大きな対称形状の単一ユニットセルをシミュレートするのに便利です。
コンピュータ・リソース
FDTDは計算集約的な手法であり、ほとんどの妥当な計算には、高速なコンピュータと少なくとも数ギガバイトのコンピュータ・メモリが必要です。ほとんどのアプリケーションでは、計算に必要なコンピュータのメモリ量を見積もるのはかなり簡単です。メモリ使用量と実行時間の大部分を左右する最も重要な要因は、 テスト対象の構造を表現するために使用する FDTD セルの数です。各 FDTD セルには、3 つの電界と 3 つの磁界の合計 6 つの電界値が関連付けられています。さらに、各セルには6つのフラグが関連付けられており、6つの電界位置のそれぞれに存在する材料タイプを示します。フィールド値は実数で、それぞれ4バイト長ですが、フラグはそれぞれ1バイトです。このため、FDTDセルあたりのメモリ使用量は、フィールドが 24バイト、フラグが6バイトで、合計30バイトとなります。必要な総メモリをバイト単位で見積もるには、単純にFDTDセル数にセルあたりの30バイトを掛ければよい。計算には若干のオーバーヘッドがあるが、一般的には非常に小さい。特筆すべき例外は広帯域のファーゾーン角度で、1 方向につき 6 つの 1 次元実数値配列が割り当てられる。
FDTD計算の実行時間の見積もりは、コンピュータ・プロセッサの性能にばらつきがあるため、より複雑になります。見積もりの1つの方法は、実行される操作の総数を計算することです。FDTD計算では、時間ステップごとにセルあたり約80回の演算が行われます。総演算回数は、セル数、時間ステップ数、時間ステップあたりのセルあたりの演算回数80回の積から求められます。
プロセッサの浮動小数点演算性能の値がわかっていれば、実行時間の値を計算することができます。しかし、一般的には、与えられたコンピュータ上で簡単な問題の実行時間を決定し、目的の計算と簡単な計算の間の演算回数の比率で時間をスケーリングするのが、より良い見積もり方法です。
FDTDの計算速度を向上させる方法は数多くあるが、プログラミングにかなりの労力を要するものもある。最も効果的なのは、コンピュータの複数のCPUを並列に使用する、複数のコンピュータを並列に使用する、計算ループをキャッシュ用に最適化する、SSEやAVXなどのCPU上の並列手法を利用する、などです。FDTDソフトウェアは、特にGPUプロセッサ上での計算に適しています。これは、多くのセルが比較的少数の更新アルゴリズムを並列に実行するという概念が、ビデオディスプレイの更新用に開発された手法によく適合しているためです。
参考文献
-
C95.3.2002, "Recommended Practice for Measurements and Computations with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 100kHz to 300GHz," IEEE Standards and Coordinating Committee 28 on Non-Ionizing Radiation Hazards, April 2002.
-
K.S. Kunz and R. J. Luebbers, "The Finite Difference Time Domain Method for Electromagnetics," Boca Raton, FL:CRC Press, 1993.

ウェビナー
NB-IoTカバレッジを地方に拡大するためのLEO衛星の利用をシミュレーション
本講演では、レムコムがWireless InSite®レイトレーシング・シミュレーション・ソフトウェアを用いて、地上波の5GカバレッジをLEO衛星リンクで補完し、地方におけるNB-IoTカバレッジを改善する方法を予測した結果を紹介する。
探索 リソース
出版物
XFdtd®の新機能
XFdtdリリース7.11.1では、シミュレーション精度の向上、解析機能の拡張、エンジニアリングワークフローの効率化を目的とした機能強化が行われています。このリリースは、アンテナ設計、PCBモデリング、フェーズドアレイシステム開発における価値の高い課題を解決するためのRemcomの継続的な取り組みを反映しています。
探索 リソース
ウェビナー
タイムベース・モビリティを用いた動的RFシナリオのモデリングとシミュレーション
強力な無線予測およびシミュレーション・プラットフォームであるWireless InSiteを使用した、動的なRF環境のモデリングについて詳しくご紹介します。視聴者は、地上通信システムから月面ミッションまで幅広いアプリケーションをサポートする、ユーザー定義シーン内でのトランシーバー、アンテナ、オブジェクトの動きをシミュレーションする方法を学ぶことができます。
探索 リソース