この例は、導電性球体からの散乱に対するXFdtdの精度を示しています。入射平面波からのバイスタティック散乱パターンが単一周波数で計算されます。
球は完全導電性で直径254mmとする。球体は原点を中心とし、図1に示すように+X方向から平面波が入射する。遠視野バイスタティックRCSパターンは、図1の赤丸で示すように、XY平面上の球を囲む円弧で計算されます。平面波は図の右側に黄色の矢印で示されており、電界はY軸に沿っている。入力信号は10GHzの正弦波である。
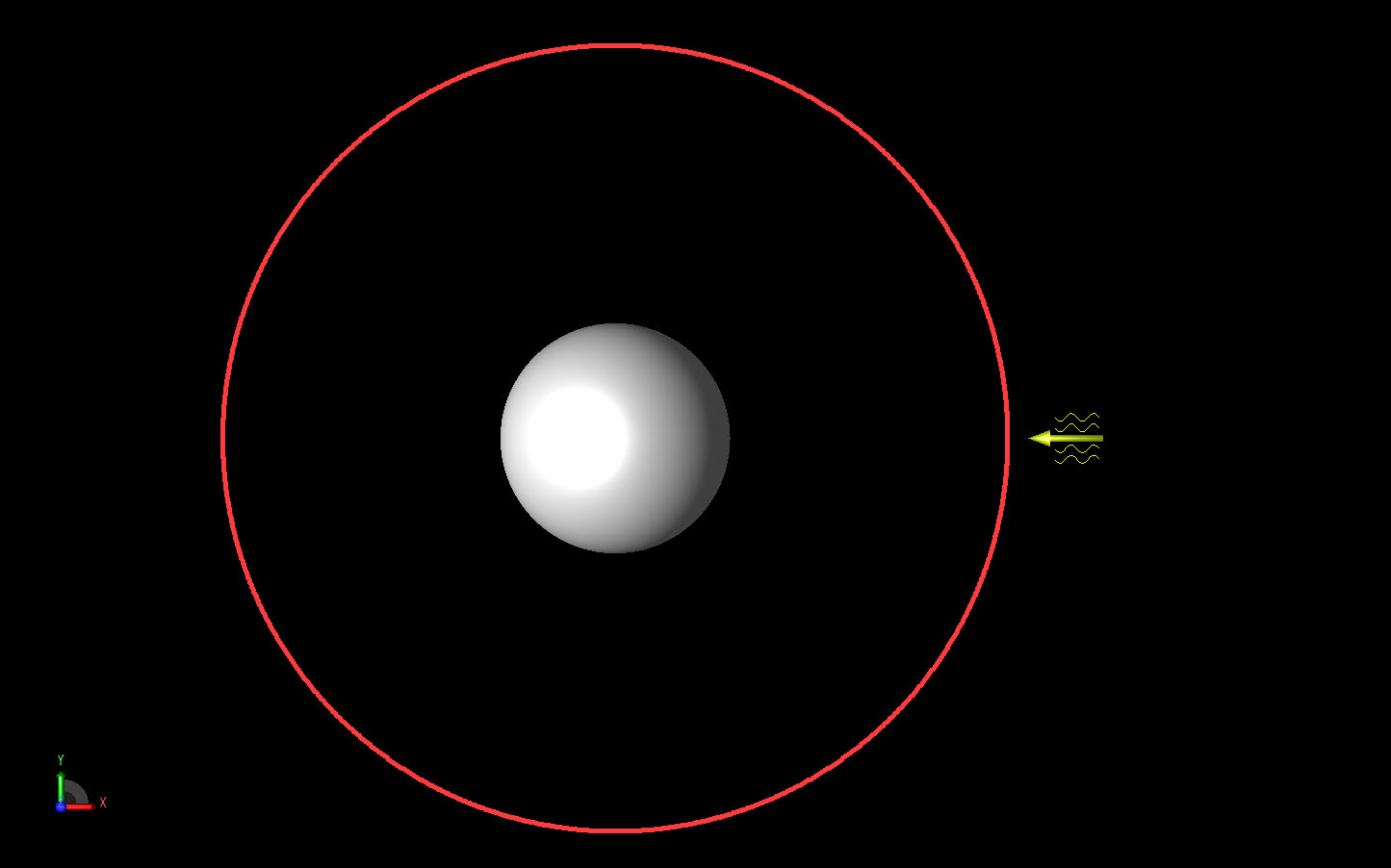
図1：球の形状を示し、入射平面波は右の黄色い矢印で表示されている。赤い円は、XY平面で計算される遠視野パターンを表す。
球体は、図2に示すように、1波長あたり30セルに相当する1mmのセルサイズのFDTDグリッドでメッシュ化される。20個のFDTDセルが物体を取り囲み、7個の完全一致層（PML）を使用した外側の境界でフィールドを吸収します。このプロジェクトの実行には、約 965 MB のメモリが必要です。
図2：セルサイズ1mmのFDTDグリッドでメッシュ化された球体。
シミュレーションは、ソフトウェアのScattered Field定式化を使用し、2.80GHzのIntel Core i7-2640M CPUで実行される。シミュレーションの実行時間は約21分です。結果として得られた前方方向のバイスタティック散乱パターンを、発表された論文[1]の測定結果と比較したところ、図3に見られるように非常によく一致しました。図4には、完全なバイスタティック散乱パターンをXY周りの極座標プロットとして示しています。図5、図6、図7にバイスタティックパターンの三次元図を示す。図8と図9では、球の中心を通過する面内の過渡電界が2つの時間インスタンスで表示されている。図8では、入射した平面波が球に入射しているが、表面の周囲を完全に伝播していない。図9では、入射平面波が球を完全に飲み込み、定常状態の電界パターンが示されている。
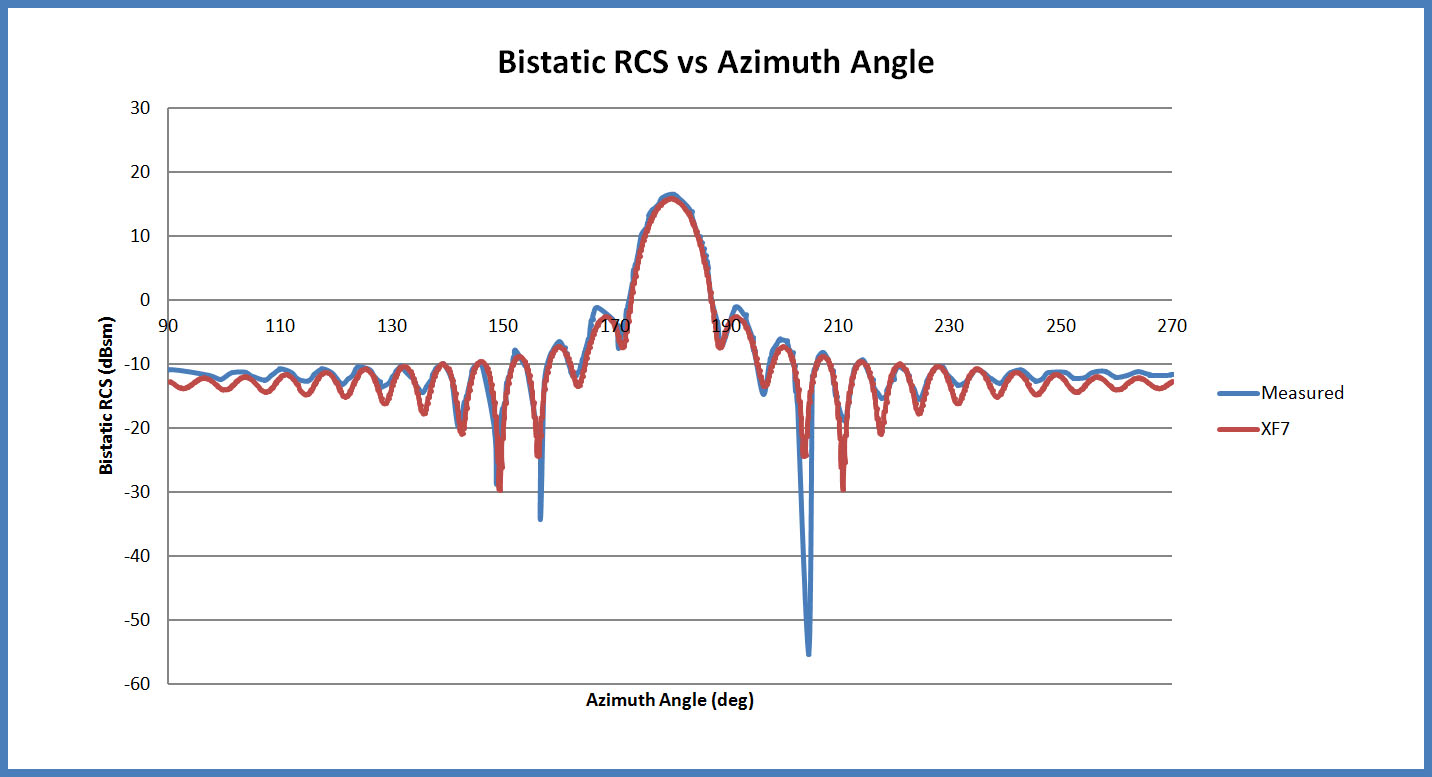
図3：前方散乱方向について、計算されたバイスタティック・レーダー断面積と測定結果の比較。優れた一致が見られる。
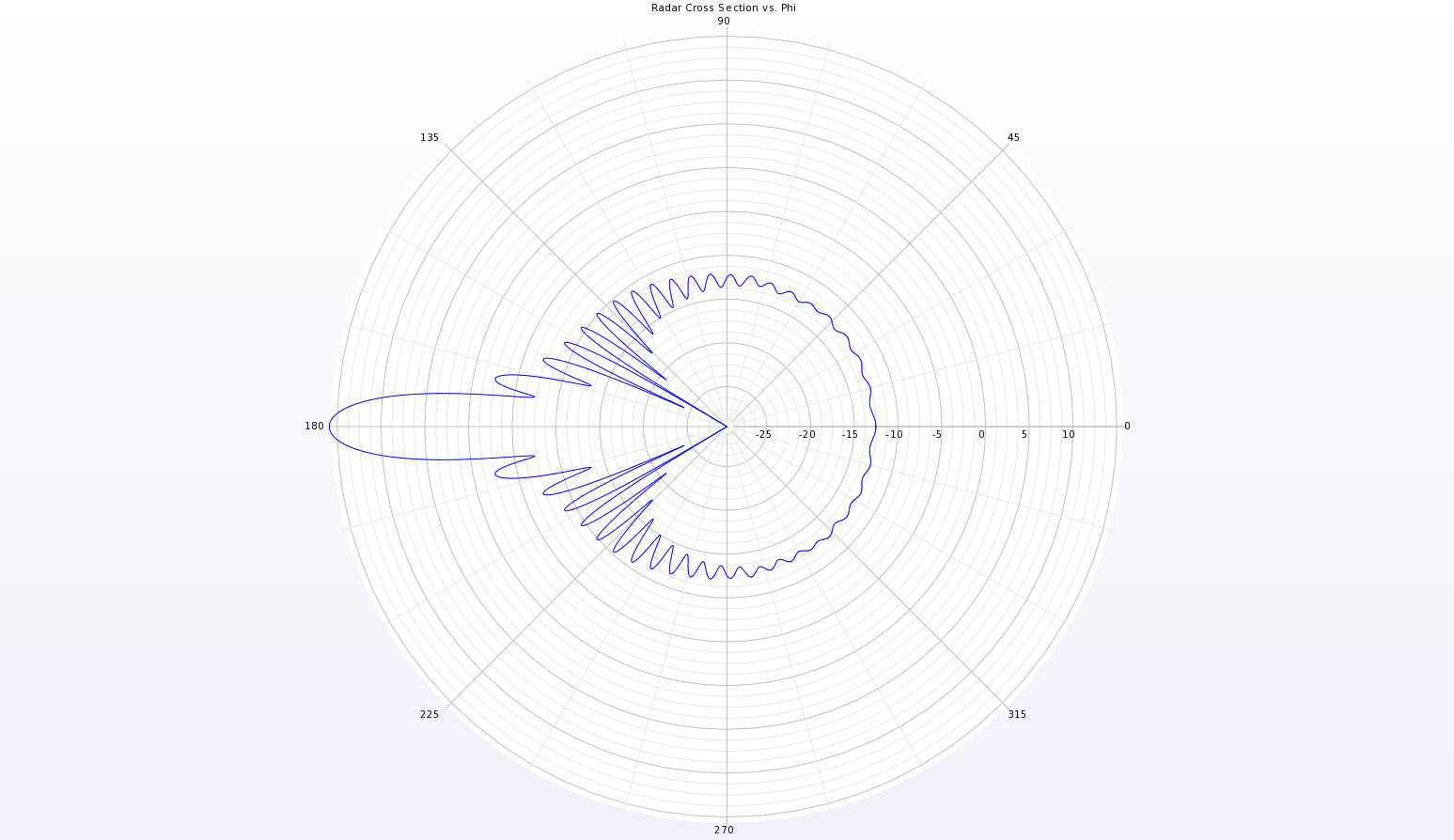
図4：球体のバイスタティック散乱パターンのXY平面における完全な極座標プロット。
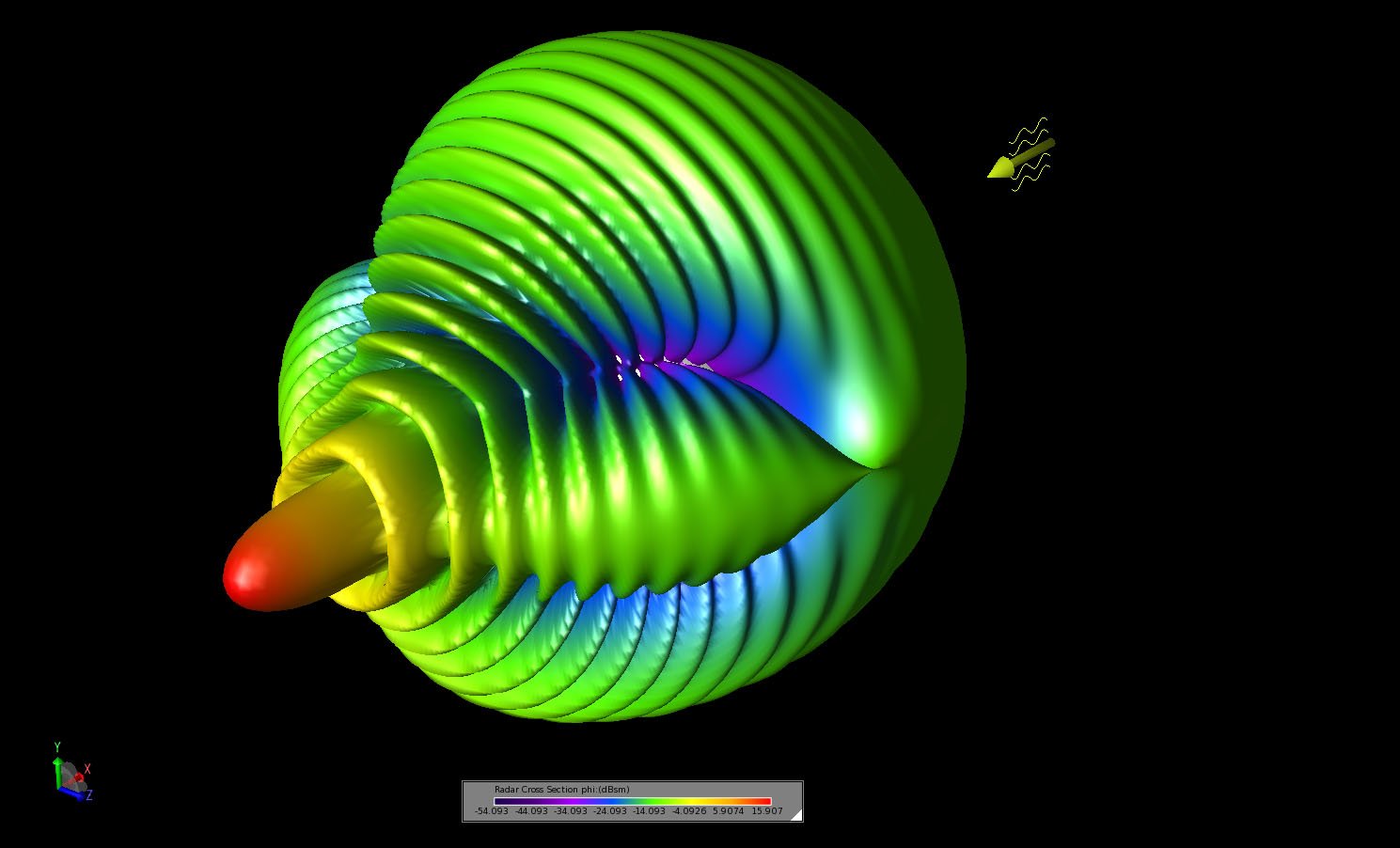
図5】パターンの前方端で角度をつけて見たところから見た、バイスタティック散乱パターンの三次元図。
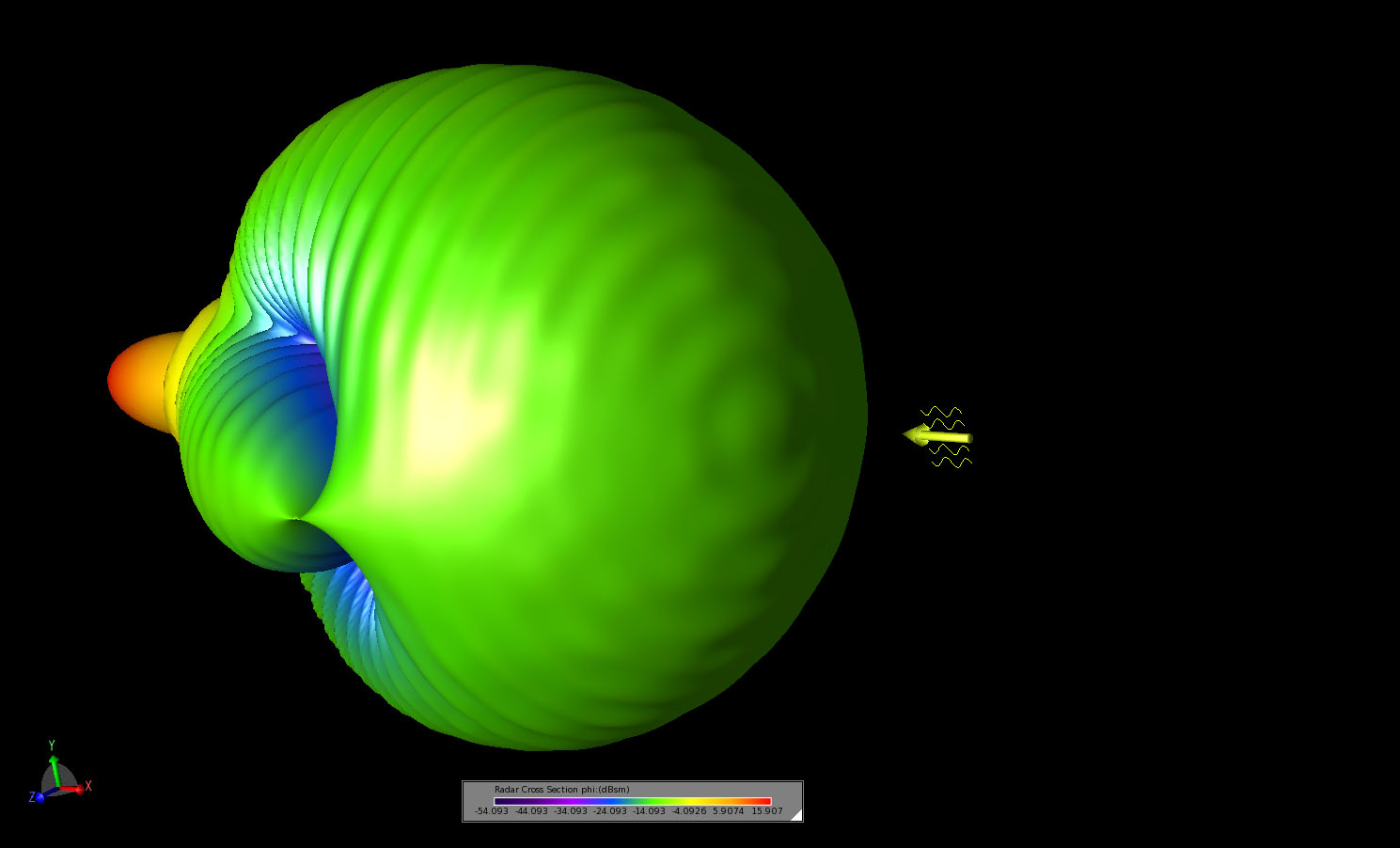
図6】パターンの後方散乱方向に角度をつけた観察位置から示したバイスタティック散乱パターンの立体図である。
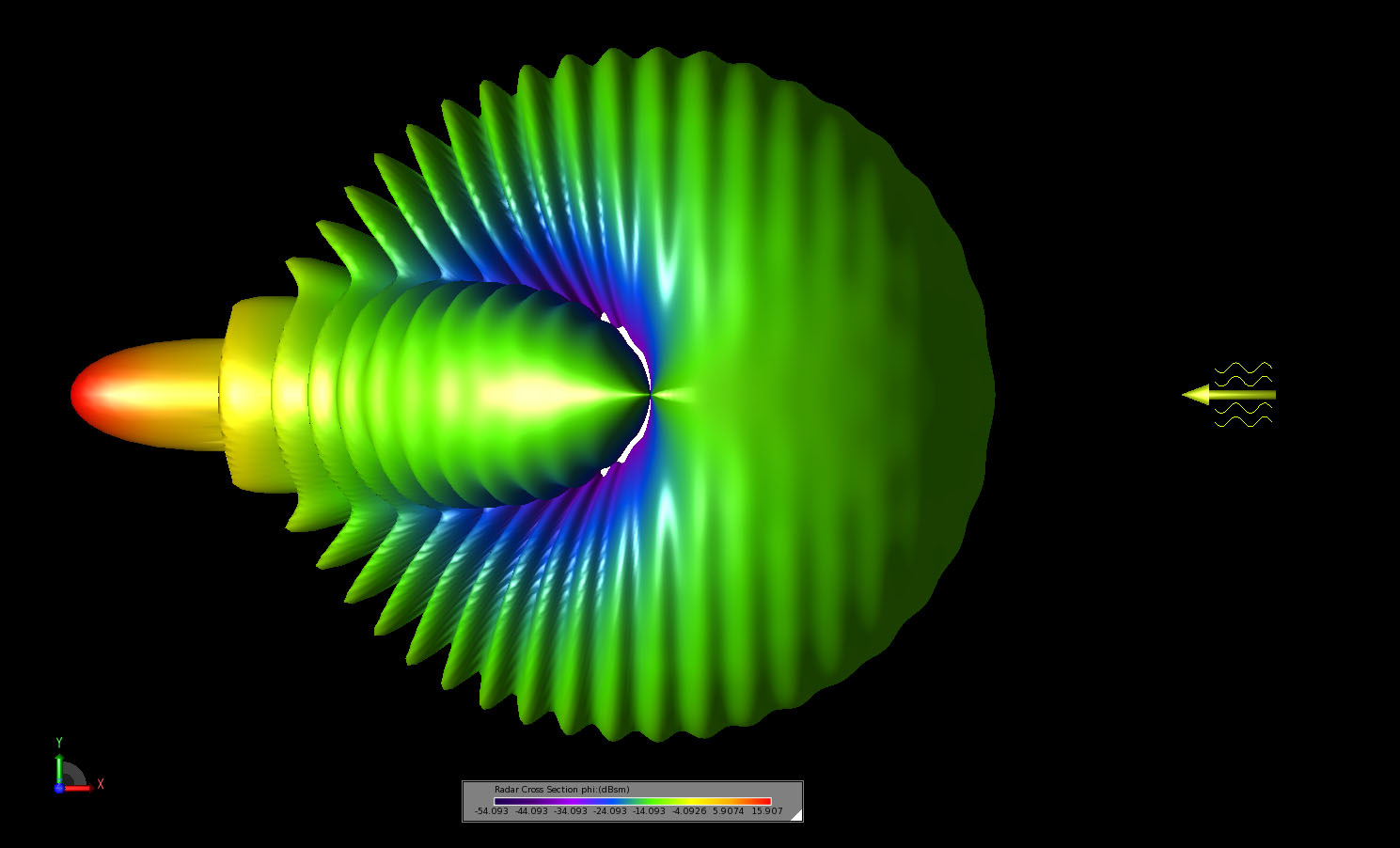
図7：XY平面に示されたバイスタティック散乱パターンの3次元図。
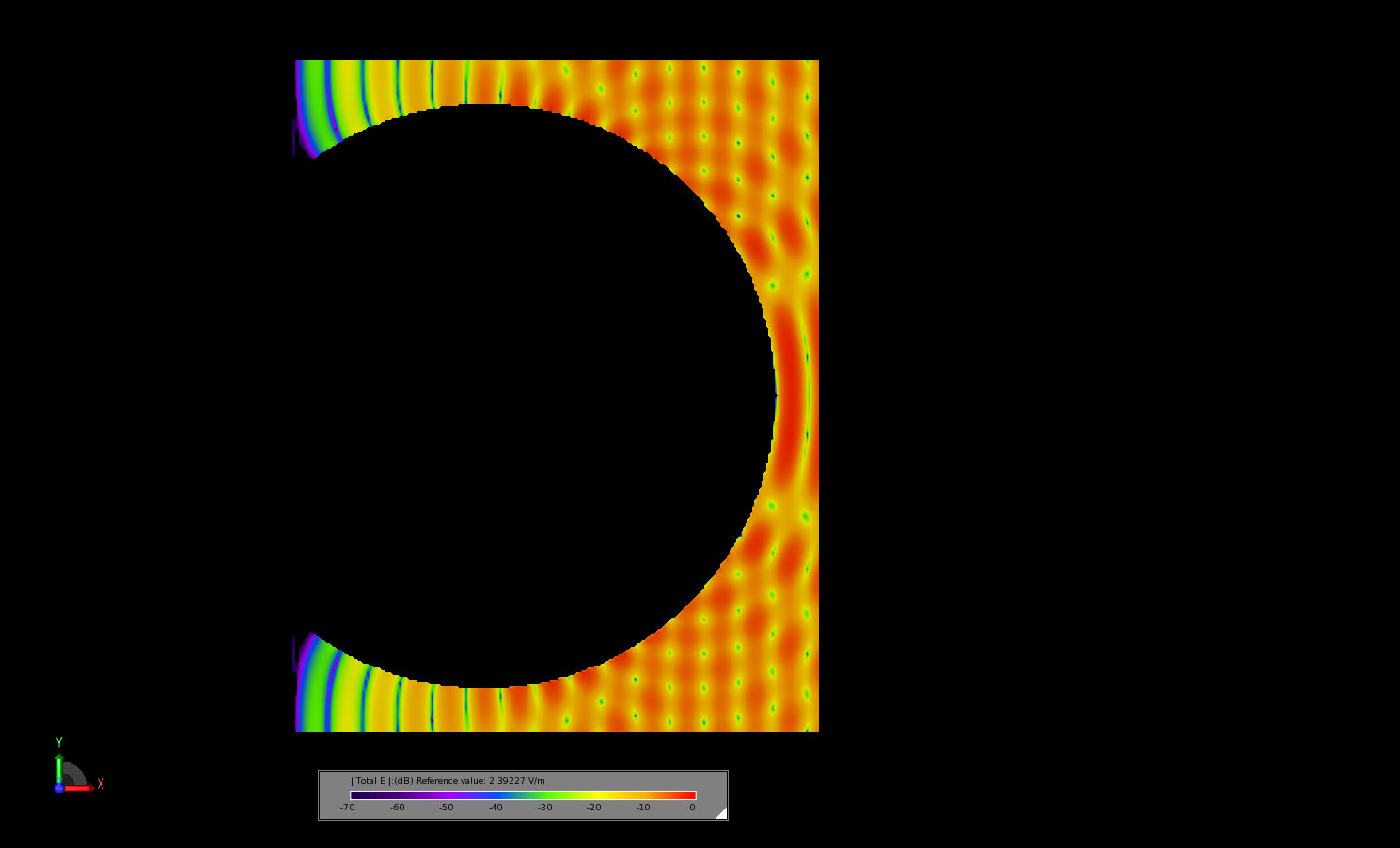
図8：入射平面波が球面に衝突し、電界が球面の周囲を伝搬しているときの、球面の中心を通るスライスにおける過渡電界を示す。
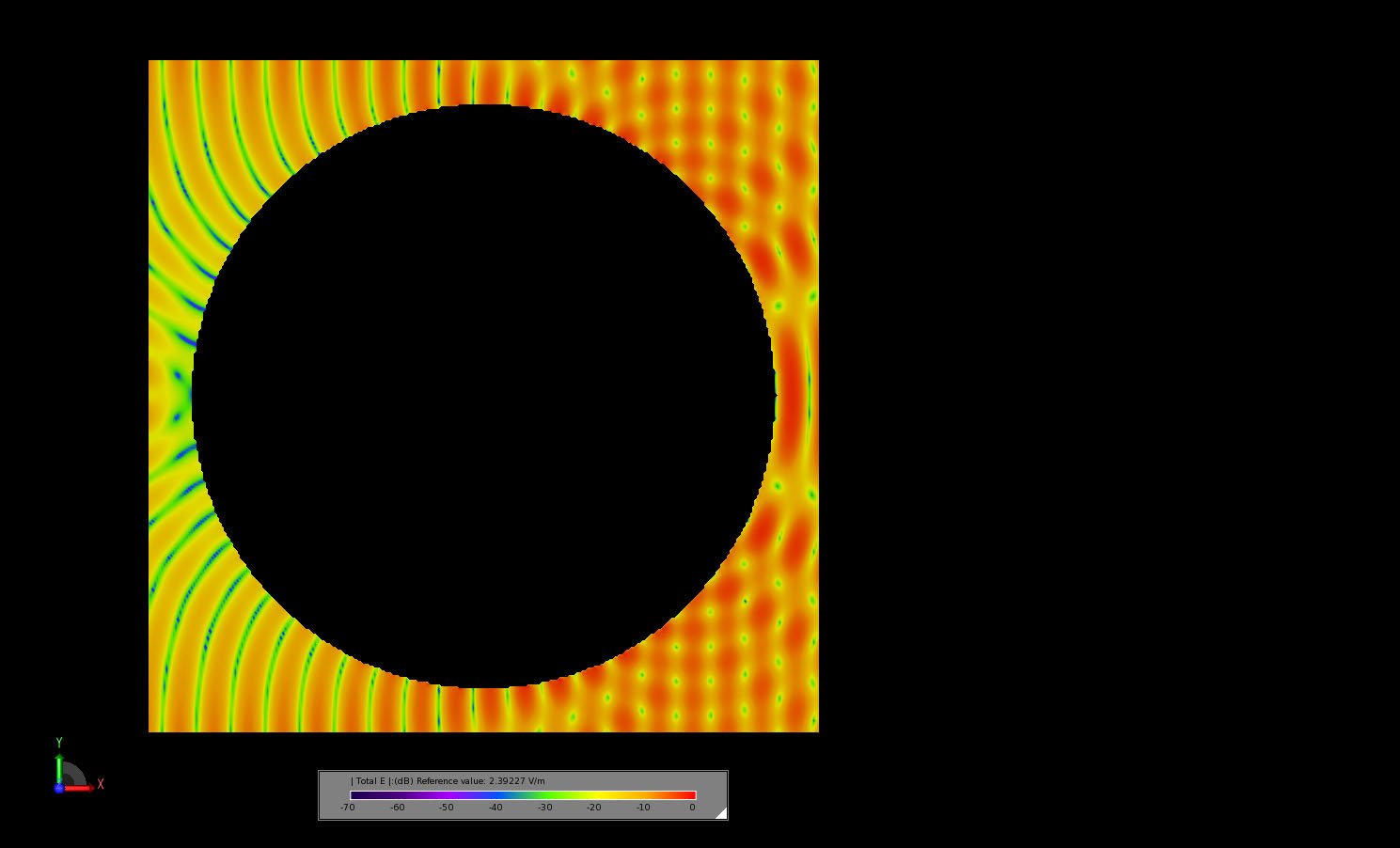
図9：電界が定常状態に達したときの球の中心を通るスライスにおける過渡電界。
参考文献
-
R.このため、このような測定は、アンテナを使用し て測定した電波を、アンテナを使用して測定した電波と比較することで、より正確な測定が可能である。Antenna Propag., Vol. 54, Dec. 2006, pp.
